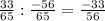Question

If A= arcsin(-4/5) in Quadrant IV and B=arctan(5/12) in Quadrant III, what is the values of tan(arcsin(-4/5)+arctan(5/12))? ASAP please...

Answer 1

pie/6

Explaniation:

just took the test on k12

Answer 2

-33/56

Explanation:

suppose: A,B are the 2 angles of a triangle

we have: A = arcsin
`(-4)/(5)`

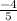
B = arctan
`(5)/(12)`

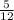
=> sin A =
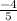`(-4)/(5)` => cos A =
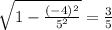`\sqrt{1-((-4)^(2) )/(5^(2) ) } =(3)/(5)` (because A is in quadrant IV)

tan B =
`(5)/(12)`

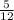
have:

`1+ cot^(2)B=(1)/(sin^(2)B ) => 1+(1)/(tan^(2) B)=(1)/(sin^(2)B ) \\=> 1+(1)/((5^(2) )/(12^(2) ) ) =(1)/(sin^(2)B )\\ => sin^(2)B=(25)/(169)`

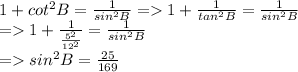
because B is in quadrant III =>
`sin B=-\sqrt{(25)/(169) }=(-5)/(13)=>cosB=-\sqrt{1-(5^(2) )/(13^(2) ) }=(-12)/(13)`

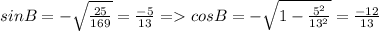
tan(arcsin(-4/5)+arctan(5/12)) = tan( A + B)

but A,B are the 2 angles of a triangle => tan(A + B) =
`(sin(A+B))/(cos(A+B))`

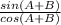
have: sin(A+B) = sinA.cosB + cosA.sinB =
`(-4)/(5).(-12)/(13) +(3)/(5).(-5)/(13)=(33)/(65)`

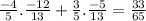
cos(A + B) = cosA.cosB - sinA.sinB =
`(3)/(5).(-12)/(13)-(-4)/(5).(-5)/(13)=(-56)/(65)`

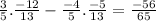
=> tan(A + B) =
`(33)/(65):(-56)/(65)=(-33)/(56)`