Question

Mike owes his friend $4. Each day, Mike earns $2.

(1) Write an equation that describes the situation in slope-intercept form and explain what the x- and y-values represent.

(2) Graph the situation on a coordinate plane assuming the domain is all real numbers.

(3) What does the x-intercept mean? What does the y-intercept mean?

(4) Does the situation involve direct variation or not? If it does, justify your answer. If it does not, describe how the situation would need to change in order for y to directly vary with x. Then, write a direct variation equation based upon the changed situation.

Answer 1

Answer && Step-by-step explanation:

We know that an equation can be used, 2*x=4

slope int form : y=mx+b

b is not necessary here

1. 4=2x

2 represents the amount of dollars, x represents amount of days, y represents the required result

2. make y, 0: 2x=0

plug in values for x to represent y values

3. x means how much money he has and y is how many days

(x,y)

4. It does involve direct variation. y/x == k

4/2=2 which is exactly what we need to get 4

Answer 2

1)

`y=2x-4`

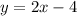
2)

Please see below for the graphs.

3)

The x-intercept means that Mike will pay off his debt after 2 days.

The y-intercept means that Mike initially owes his friend $4.

4)

No, it does not involve direct variation.

We can change it to direct variation if we remove the debt Mike owes.

The direct variation equation will then be:

`y=2x`

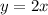
Explanation:

We know that Mike owes his friend $4. Each day, Mike earns $2.

Part 1)

Let y represent the amount of money Mike will have after x days.

Since Mike owes his friend $4, this means that the original amount he has is -4.

However, Mike earns $2 per day. So, our slope will be +2x.

Putting this all together, the equation that represents Mike’s situation is:

`y=2x-4`

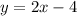
The y represents Mike’s total assets (money). The -4 represents what Mike started with, he $4 he owes. And the 2x represents the amount Mike will have after x days since he earns $2 per day.

Part 2)

Please see the graph below.

To graph by hand, first start by drawing a dot at the y-intercept, (0, -4).

Now, since our slope is 2, this is the same as saying 2/1.

So, draw a dot by going up 2 for every 1 right. Do this at least twice. This should yield three dots.

Finally, connect them with a graph.

I’ve also done it by hand to give you a visual.

Part 3)

So, from the graph, we can see that the x-intercept is (2, 0).

And the y-intercept is (0, -4).

The x-intercept tells us that when x is 2, y is 0.

Therefore, this means that after two days, Mike would’ve paid off his debt of $4.

Similarly, our y-intercept tells us that when x is 0, y is -4.

So, on Day 0, when Mike haven’t earned any money yet, he owes $4 as illustrated by -4.

Part 4)

Remember that direct variation equations must always go through the origin point.

Since our equation does not go through the origin, our equation is not direct variation.

Remember that for a graph to be direct variation, the y-intercept must be 0.

In other words, if Mike doesn’t owe any money at the start, we will have direct variation.

Thus, if the situation changed such that Mike doesn’t owe his friend any money, then we will have a direct variation equation.

Since he doesn’t owe any money, our y-intercept is 0. He will still earn $2 per day. Therefore, our equation will be:

`y=2x`

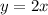
Here, our constant of variation is 2, illustrating that Mike earns $2 per day.

And we are done!