Answer:
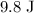 , assuming that the gravitational field strength is
, assuming that the gravitational field strength is
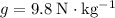 .
.
Step-by-step explanation:
Notice that both the speed and the direction of motion of this block are constant. In other words, the velocity of this block is constant.
By Newton's Second Law, the net force on this block would be
 . External forces on this block should be balanced. Thus, the magnitude of the (downward) weight of this block should be equal to the magnitude of the (upward) force that the boy applies on this block.
. External forces on this block should be balanced. Thus, the magnitude of the (downward) weight of this block should be equal to the magnitude of the (upward) force that the boy applies on this block.
Let
 denote the mass of this block. It is given that
denote the mass of this block. It is given that
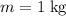 . The weight of this block would be:
. The weight of this block would be:
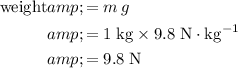 .
.
Hence, the force that the boy applies on this block would be upward with a magnitude of
 .
.
The mechanical work that a force did is equal to the product of:
- the magnitude of the force, and
- the displacement of the object in the direction of the force.
The displacement of this block (upward by
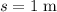 ) is in the same direction as the (upward) force that this boy had applied. Thus, the work that this boy had done would be the product of:
) is in the same direction as the (upward) force that this boy had applied. Thus, the work that this boy had done would be the product of:
- the magnitude of the force that this boy exerted,
 , and
, and - the displacement of this block in the direction,
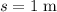 .
.
 .
.