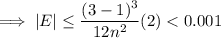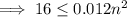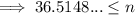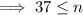Question

Someone please help

Answer 1

Part (a)

Given:

`\displaystyle \int\limits_(1)^(3) x^2 \:dx`

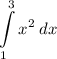
Trapezium Rule

`\displaystyle \int\limits_(a)^(b) y \:dx \approx (1)/(2)h\left[(y_0+y_n)+2(y_1+y_2+...+y_(n-1))\right] \quad \textsf{where }h=(b-a)/(n)`

Calculate the width of each strip (h).

Given:

• a = 1
• b = 3
• n = 5

`\implies h=(3-1)/(5)=0.4`

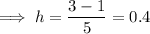
Create a table with the x and y values:

`\large\begin{array} c \cline{1-7} x & 1 & 1.4 & 1.8 & 2.2 & 2.6 & 3\\\cline{1-7} y & 1 & 1.96 & 3.24 & 4.84 & 6.76 & 9\\\cline{1-7}\end{array}`

Put all the values into the formula:

`\begin{aligned}\displaystyle \int\limits_(1)^(3) x^2 \:dx & \approx (1)/(2)(0.4)\left[(1+9)+2(1.96+3.24+4.84+6.76)\right]\\& = 0.2\left[10+2(16.8)\right]\\\\& = 0.2\left[10+33.6\right]\\\\& = 0.2\left[43.6\right]\\\\& = 8.72 \end{aligned}`

Part (b)

`\begin{aligned}\displaystyle \int\limits_(1)^(3) x^2 \:dx &=\left[(1)/(3)x^3\right]^3_1\\& = (1)/(3)(3)^3-(1)/(3)(1)^3\\& = 9-(1)/(3)\\& = (26)/(3)\end{aligned}`

The exact area as a decimal is
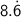`\sf 8.\dot{6}`. Therefore, the estimated answer of 8.72 is an overestimate.

Part (c)

Answer to (a) = 8.72

To find the maximum possible error:

• Identify the last non-zero digit to the right of the decimal point → 2
• The precision of the number is the place value: 0.01
• Divide the precision by 2

Therefore, the maximum possible error for 8.72 is 0.005.

Part (d)

Trapezoid Error formula

`|E| \leq ((b-a)^3)/(12n^2)\left[\textsf{max}|f''(x)|\right],\quad a \leq x \leq b`

Calculate the second derivative:

`f(x)=x^2`

`f'(x)=2x`

`f''(x)=2`

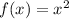
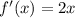
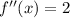
Input the values into the formula:

`\implies |E| \leq ((3-1)^3)/(12n^2)(2) < 0.001`

`\implies 16 \leq 0.012n^2`

`\implies 36.5148...\leq n`

`\implies 37\leq n`