Answer:
The wait time is unusual because the probability value obtained is less than 2 standard deviation above the mean
Explanation:
From the question we are told that
The average wait time is
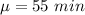
The standard deviation is
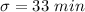
Generally the probability of waiting over 1212 minutes is
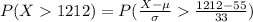
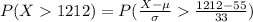
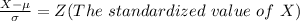
So
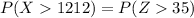
From z table the probability of (Z > 35 ) is
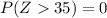
Hence
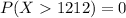
The time is unusual because the probability value obtained is less than 2 standard deviation above the mean