Question

A bucket that weighs 4 lb and a rope of negligible weight are used to draw water from a well that is 60 ft deep. The bucket is filled with 38 lb of water and is pulled up at a rate of 2.5 ft/s, but water leaks out of a hole in the bucket at a rate of 0.25 lb/s. Find the work done in pulling the bucket to the top of the well.

Answer 1

The work-done required to pull the bucket to the top of the well = 2340 ft-lb

Explanation:

From the information given:

The water is pulled at a rate of 2.5 ft/s

Also, water leaks out of a hole in the bucket at a rate of 0.25 lb/s.

Thus, the rate of water leaking out of the bucket is:

`(0.25 \ lb/s)/(2.5 \ ft/s)`

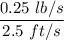
= 0.1 lb/ft

The work done needed to pull the bucket to the top of the well can be expressed by using the integral:

`W = \int ^b_a F(x) \ dx`

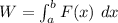
where;

F(x) is read as the function of x = total weight of the bucket and water

i.e

F(x) = 4 + ( 38 - 0.1x)

F(x) = 42 - 0.1x

and a which is inital height = 0 and b which is th final height = 60

Thus: we can compute the workdone as follows:

`W = \int^b_a F(x) \ dx`

`W = \int^(60)_0 (42-0.1x) \ dx`

`W =\int ^(60)_(0) \begin {pmatrix} (42 x)/(1)- (0.1x^2)/(2) \end {pmatrix} \ dx`

`W =\ \begin {pmatrix} 42x- 0.05x^2\end {pmatrix} |^(60)_(0)`

`W =\ \begin {pmatrix} 42(60)- 0.05(60)^2\end {pmatrix}-0`

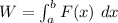
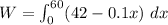
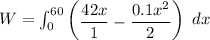
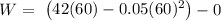
W = 2520 - 180

W = 2340 ft-lb