Answer: The value of h that maximizes the volume of the box is h = 3.36
Explanation:
First, the volume of a box of length L, width W, and height H is:
V = L*W*H.
in this case, we start with a rectangle of measures AxB.
We can define that the side with length A will be the length, and the other side will be the width.
As we cut squares of length h in the corners, now we will have that the measures of the box are:
Length = A - 2*h
Width = B - 2*h
Height = h.
And we know that A = 17 and B = 27.
So we can replace those values and get:
Length = 17 - 2*h
Width = 27 - 2*h
Height = h
The volume of this box will be:
V = (17 - 2*h)*(27 - 2*h)*h = 459*h -54*h^2 - 34*h^2 + 4*h^3.
Now we want to maximize this.
V(h) = 4*h^3 - 88*h^2 + 459*h
To find the maximum, let's look at the first derivation of V(h)
V'(h) = 3*4*h^2 - 2*88*h + 459.
We need to look for which values of h this is zero.
0 = 12*h^2 - 176*h + 459
The solutions are given by the Bhaskara equation:
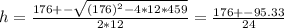
Then the two solutions are:
h = (176 + 95.33)/24 = 11.3
h = (176 -95.33)/24 = 3.36
Now, the problem with the first solution is that if we cut two squares of length 11.3 in side A (2*11.3 > 17) , the amount of material cut is larger than A, so that option can be discarded.
Then the only option is h = 3.36
The value of h that maximizes the volume of the box is h = 3.36