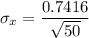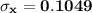Answer:
The standard deviation of the sample mean
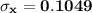
Explanation:
We are provided with just a question; so, we are going to do just that.
Given that:
The population Mean
 = 3.15
= 3.15
The population variance
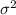 = 0.55
= 0.55
The sample size n = 50
We can calculate the Standard deviation of the sample mean
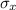 by using the formula:
by using the formula:
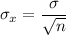
Recall that:
The population variance
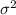 = 0.55
= 0.55
So;
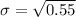
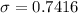
Then: