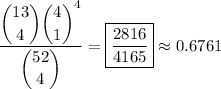Question

If you draw four cards at random from a standard deck of 52 cards, what is the probability that all 4 cards have distinct characters (letters or numbers)

Answer 1

There are
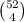`\binom{52}4` ways of drawing a 4-card hand, where

`\dbinom nk = (n!)/(k!(n-k)!)`

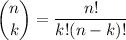
is the so-called binomial coefficient.

There are 13 different card values, of which we want the hand to represent 4 values, so there are
`\binom{13}4` ways of meeting this requirement.

For each card value, there are 4 choices of suit, of which we only pick 1, so there are
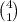`\binom41` ways of picking a card of any given value. We draw 4 cards from the deck, so there are
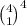`\binom41^4` possible hands in which each card has a different value.

Then there are
`\binom{13}4 \binom41^4` total hands in which all 4 cards have distinct values, and the probability of drawing such a hand is

`\frac{\dbinom{13}4 \dbinom41^4}{\dbinom{52}4} = \boxed{(2816)/(4165)} \approx 0.6761`