Question

A business has seven locations to choose from and wishes to rank only the top three locations. How many different ways can this be done?

Answer 1

Answer: 210

Explanation:

Given: total locations = 7

Number of locations wishes to rank = 3

If order of selection matters, then the number of permutations of r things from n=
`(n!)/((n-r)!)`

The number of ways to rank 3 locations out of 7
`=(7!)/((7-3)!)=7*6*5=210`

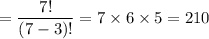
Hence, the number of different ways required = 210