Question

3. The daily surface concentration of carbonyl sulfide on the Indian Ocean is normally distributed, with a mean of 9.1 picomoles per liter and a standard deviation of 3.5 picomoles per liter. Find the probability that on a randomly selected day, the surface concentration of carbonyl sulfide on the Indian Ocean is less than 13.5 picomoles per liter.

Answer 1

Answer: 0.8956

Explanation:

Given: The daily surface concentration of carbonyl sulfide on the Indian Ocean is normally distributed, with a mean
`\mu=100` picomoles per liter and standard deviation of
`\sigma=3.5` picomoles per liter.

Let X be the daily surface concentration of carbonyl sulfide.

The probability that on a randomly selected day, the surface concentration of carbonyl sulfide on the Indian Ocean is less than 13.5 picomoles per liter
`= P(X<13.5)`

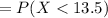
`=P((X-\mu)/(\sigma)>(13.5-9.1)/(3.5))\\\\=P(Z<1.257)\\\\= 0.8956\ \ \ [\text{By p-value table}]`

Hence, the required probability = 0.8956