Answer:
Explanation:
In the question, it is given that a right cone has a diameter of 12 units and volume of 168π units³ and we have to find the height of the cone.

To Find the height of the cone, we must know this formula :
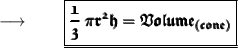
Where,
- r refers to the radius of the cone. Here, the diameter is 12, Therefore the radius will be 6 units.
- h refers to the height of the cone.
Now, we will substitute the values in the formula :
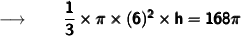
Cancelling π from both sides we get :
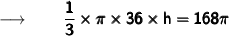
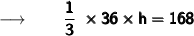
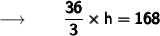
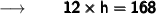


Therefore,
- The height of the cone is 14 units .