Question

Y varies inversely as x and y = 11 when x = 8. Determine the value of y when x = 16

22
5.5
17
34

Answer 1

`\qquad\qquad\huge\underline{{\sf Answer}}`

Let's get started ~

According to question :

`\sf \dashrightarrow y \propto (1)/(x)`

`\sf \dashrightarrow y = k(1)/(x)`

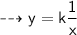
• where, k = proportionality constant

Now, we have been given that when y = 11, x = 8

Let's plug these values in equation to find value of k ~

`\sf \dashrightarrow 11 = k \cdot(1)/(8)`

`\sf \dashrightarrow k = 11 * 8`

`\sf \dashrightarrow k =88`

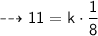
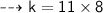
we got the value of proportionality constant. now we have been asked to find the value of y when x = 16

So, let's use the equation ~

`\sf \dashrightarrow y = k \cdot(1)/(x)`

`\sf \dashrightarrow y = 88\cdot(1)/(16)`

`\sf \dashrightarrow y = (11)/(2)`

`\sf \dashrightarrow y = 5.5`

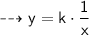
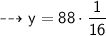
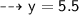
I hope you understood the whole procedure ~