Question

2. A rocket, with an initial mass of 800 kg, is to be launched vertically. Upon ignition the rocket consumes fuel at the rate of 5 kg/s and ejects gas at atmospheric pressure with a speed of 3500 m/s relative to the rocket. Determine the initial acceleration of the rocket and the rocket speed after 20 s if air resistance is neglected. [40 20 points].

Answer 1

The acceleration is
`a = 11.88 \ m/s^2`

The velocity after 20 second is
`v = 267.36 \ m/s`

Step-by-step explanation:

From the question we are told that

The mass of the rocket is
`m = 800 \ kg`

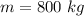
The rate of fuel consumption is
`r = 5 \ kg / s`

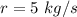
The speed of speed at which gas is ejected at atmospheric pressure is
`v_g = 3500 \ m/s`

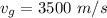
Generally the thrust force (the force propelling the rocket) is mathematically represented as

`F_1 = v_g * r`

=>
`F_1 = 3500 * 5`

=>
`F_1 = 17500 \ N`

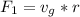
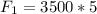
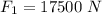
Generally the net force acting on the rocket is mathematically represented as

`F_(net) = F_1 - mg`

=>
`m * a = 17500 - (800 * 9.8)`

=>
`800 * a = 17500 - (800 * 9.8)`

=>
`a = 11.88 \ m/s^2`

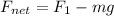
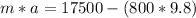
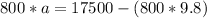
Generally the rocket speed is mathematically represented as

`v = v_i - gt + v_g * ln[(m)/(m_r) ]`

Here
`v_i` is the initial velocity of the rocket which is 0 given that it started from rest

`m_r` of the rocket after fuel has been consumed for time t = 20

second, this mathematically represented as

`m_r = m - (r * t )`

=>
`m_r =800 - (5 * 20 )`

=>
`m_r = 700 \ kg`

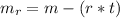
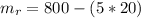
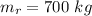
So

`v = 800 - 9.8 * 20 + 3500 * ln[(800)/(700) ]`

=>
`v = 267.36 \ m/s`