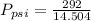Complete Question
The complete question is shown on the first uploaded image
Answer:
a

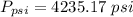
b
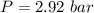
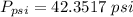
c


Step-by-step explanation:
From the question we are told that
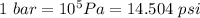
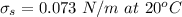
Generally the pressure difference is mathematically represented as
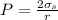
Considering question a
Here the diameter is
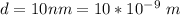
Generally the radius is mathematically represented as
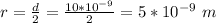
So
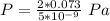
=>
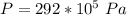
Converting to bar
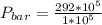

Converting to psi
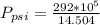
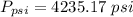
Considering question b
Here the diameter is

Generally the radius is mathematically represented as
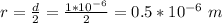
So
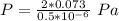
=>
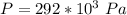
Converting to bar
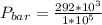
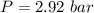
Converting to psi
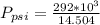
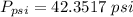
Considering question c
Here the diameter is
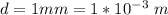
Generally the radius is mathematically represented as
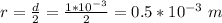
So
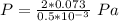
=>

Converting to bar
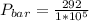

Converting to psi