Answer: 0.04848
Explanation:
Given : There are 4 sophomores, 4 juniors and 3 seniors.
Total choices = 4+4+3 = 11
Number of people needed to be chosen for committee = 4
Number of ways to select 3 people out of 11 (without replacement)=
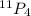
![=(11!)/((11-4)!)\ \ \ \ [^nP_r=(n!)/((n-r)!)]](https://img.qammunity.org/2021/formulas/mathematics/college/hhvqnet0gyen354gqr8rfz2fp5kwjsw61j.png)
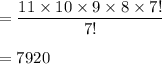
Number of ways to select at least one representative from all three groups of students =
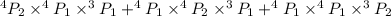
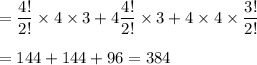
Required probability =
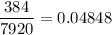
Hence, the probability the committee thus formed will have at least one representative from all three groups of students = 0.04848