Answer:
The expression for the required minimum sample size is
![n=[(1.645*\sigma )/(D)]^(2)](https://img.qammunity.org/2021/formulas/mathematics/college/9evacs56qa1m31opfz2olkxvr3nutrw57m.png) .
.
Explanation:
The (1 - α) % confidence interval for population mean is:
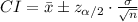
The margin of error for this interval is:
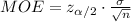
Confidence level = 90%
α = 10%
Compute the critical value of z for α = 10% as follows:
z = 1.645
*Use a z-table.
Compute the sample size required as follows:
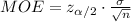
![n=[(z_(\alpha/2)*\sigma )/(MOE)]^(2)](https://img.qammunity.org/2021/formulas/mathematics/college/iscoagw4gqumv14h5b5qu6ldt12ejqo5jy.png)
![n=[(1.645*\sigma )/(D)]^(2)](https://img.qammunity.org/2021/formulas/mathematics/college/9evacs56qa1m31opfz2olkxvr3nutrw57m.png)
Thus, the expression for the required minimum sample size is
![n=[(1.645*\sigma )/(D)]^(2)](https://img.qammunity.org/2021/formulas/mathematics/college/9evacs56qa1m31opfz2olkxvr3nutrw57m.png) .
.