Question

Use Lagrange multipliers to find the absolute maximum value and absolute minimum value of f(x, y) = 2x 2 + 2y subject to x 2 + 2y + y 2 = 15.

Answer 1

Maximum absolute value of f=61/2 at (
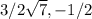`3/2√(7),-1/2`) and (
`-3/2√(7),-1/2`)

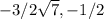Minimum absolute value of f=-10 at (0,-5)

Explanation:

We are given that

`f(x,y)=2x^2+2y`

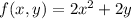
Let

`g(x,y)=x^2+2y+y^2-15=0`

`\\abla f(x,y)=<4x,2>`

`\\abla g(x,y)=<2x,2+2y>`

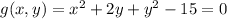
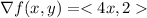
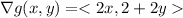
Using Lagrange multipliers

`f_x(x,y)=\lambda g_x(x,y)`

`4x=2x\lambda`

`4x-2x\lambda=2x(2-\lambda)=0`

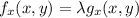
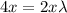
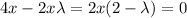
x=0 or

`\lambda=2`

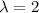
If x=0

Then,

`y^2+2y-15=0`

`y^2+5y-3y-15=0`

`y(y+5)-3(y+5)=0`

`(y+5)(y-3)=0`

`y=-5,3`

`2=(2+2y)\lambda`

If
`\lambda=2`

`2=2(2+2y)`

`2/2=2+2y`

`1=2+2y`

`2y=1-2=-1`

`y=-(1)/(2)`

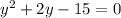
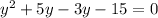
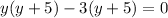
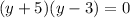
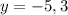
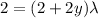
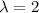
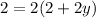
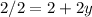
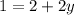
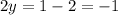
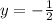
If y=-1/2

Then,

`x^2-1+1/4=15`

`x^2+((-4+1)/(4))=15`

`x^2-(3)/(4)=15`

`x^2=15+3/4=(60+3)/(4)=(63)/(4)`

`x=\pm(3√(7))/(2)`

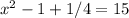
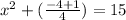
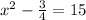
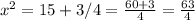
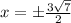
Therefore, possible extreme points are

(0,-5),(0,3),(
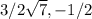`3/2√(7),-1/2`) and (
`-3/2√(7),-1/2`)

`f(0,-5)=2(0)+2(-5)=-10`

`f(0,3)=2(3)=6`

`f(3/2√(7),-1/2)=(63)/(2)-1=(61)/(2)`

`f(-3/2√(7),-1/2)=(63)/(2)-1=(61)/(2)`

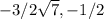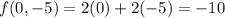
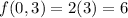
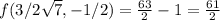
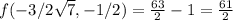
Therefore, maximum absolute value of f=61/2 at (
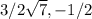`3/2√(7),-1/2`) and (
`-3/2√(7),-1/2`)

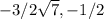Minimum absolute value of f=-10 at (0,-5)