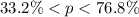1 Answer

Liam Neesan · Answer 1 · 2021-01-24T11:34:10+0000

Complete Question

The data for this question is shown on the first uploaded image

Answer:

The 95% confidence interval estimate of the population percentage is

$33.2\% <  p < 76.8 \%$

Explanation:

On the data the first value is the height of the president while the other value is the height of his opponent

The sample size is n = 20

Looking at the data we see that out of the 20 presidents that only 11 is taller than their opponent

So the proportion of presidents that are taller than their opponents is

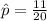
$\^ p = (11)/(20)$

=>
$\^ p = 0.55$

From the question we are told the confidence level is 95% , hence the level of significance is

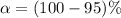
$\alpha = (100 - 95 ) \%$

=>
$\alpha = 0.05$

Generally from the normal distribution table the critical value of is

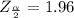
$Z_{(\alpha )/(2) } =  1.96$

Generally the margin of error is mathematically represented as

$E = Z_{(\alpha )/(2) } *  \sqrt{(\^ p (1- \^ p) )/(n)}$

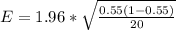
$E = 1.96 *  \sqrt{(0.55 (1- 0.55) )/(20)}$

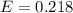
E = 0.218

Generally 95% confidence interval is mathematically represented as

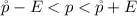
$\r p -E <  p <  \r p +E$

=>
0.55-0.218 < p < 0.55+ 0.218

=>
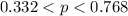
0.332 < p < 0.768

Converting to percentage

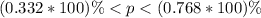
$(0.332*100)\% <  p < (0.768 *100) \%$

=>
$33.2\% <  p < 76.8 \%$

Please log in or register to add a comment.