Question

A 1.0 kg rock is dropped from a height of 6.0 m. At what height is the rock’s kinetic energy twice its potential energy? (Assume the air resistance is zero)

Answer 1

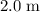`2.0\; \rm m` (which is one-third the initial height of this rock.)

Step-by-step explanation:

Let
`m` represent the mass of this rock, let
`h_0` represent the initial height of this rock, and let
`g` represent the acceleration due to gravity.

The initial potential energy of this rock would be
`m \cdot g \cdot h_0`.

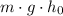The question assumed that air resistance is zero. Therefore, the mechanical energy of this rock (that is, the sum of its potential and kinetic energy) should have stayed the same during the fall.

Assume that the rock was released from rest. That way, the initial kinetic energy of this rock would be zero. The mechanical energy of this rock before the fall would be equal to the potential energy of the rock at that point:
`m\cdot g \cdot h_0`.

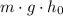Let the height of this rock be
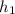`h_1` when the kinetic energy of the rock is exactly twice the potential energy of this rock. At that height, the potential energy of the rock would be
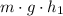`m \cdot g \cdot h_1`. The kinetic energy of the rock would be twice that amount (that is:
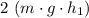`2\, \left(m \cdot g \cdot h_1\right)`.) Therefore, the mechanical energy of this rock at that moment would be
`m \cdot g \cdot h_1 + 2\, \left(m \cdot g \cdot h_1\right) = 3\, \left(m \cdot g \cdot h_1\right)`.

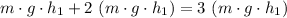Because there is no air resistance on this rock, the mechanical energy of this rock would stay unchanged during the fall:

`3\, \left(m \cdot g \cdot h_1\right) = m \cdot g \cdot h_0`.

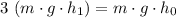Simplify this equation to obtain:

`\displaystyle h_1 = (h_0)/(3)`.

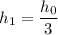In other words, when the kinetic energy of this rock is twice its potential energy, the height of this rock would be one-third of its initial height.

The initial height of this rock is
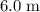`6.0\; \rm m`. One-third of that would be
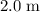`2.0\; \rm m`. That should be the height of this rock when its kinetic energy is twice its potential energy.