Question

Hello :) how to do this question?:)

Answer 1

a= 2.5, b= 5

Explanation:

Since the graph is obtained by plotting y against xy, Y= y and X= xy. (Linear law: Y=mX +c)

Given that the line intersects the vertical axis at (0, ½), the y-intercept is ½.

Equation of the line: Y= mX +½

Given that the gradient is ⅕, m= ⅕.

Y= ⅕X +½

Substitute Y= y and X=xy:

y= ⅕xy +½

Rewrite the equation such that it is in the form of
`y = (a)/(b - x)`:

`y - (1)/(5) xy = (1)/(2)`

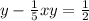
Factorise y out on the left hand side:

`y(1 - (1)/(5) x) = (1)/(2)`

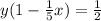
Make y the subject of formula:

`y = (1)/(2) / (1 - (1)/(5) x) \\ y = (1)/(2) / ( (5)/(5) - (x)/(5) ) \\ y = (1)/(2) / (5 - x)/(5) \\ y = (1)/(2) * (5)/(5 - x) \\ y = (5)/(2(5 - x))`

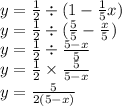
Do not expand at this step as the coefficient of x in the equation is 1. Instead, divide both the numerator and denominator by 2.

`y = (2.5)/(5 - x)`

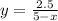
Thus, a= 2.5 and b= 5.