Answer:
D) 8 Children’s Haircuts
Explanation:
Let a represent the amount of adult haircuts and c represent the amount of child haircuts.
We know that she gave exactly 14 haircuts. So:

We also know that she made $50.00. Therefore, the price of each haircut times their respective amounts will total $50. So:
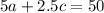
This is now a system of equations.
We can solve this using substitution. From the first equation, let’s subtract c from both sides:

Now, we can substitute this into the second equation for a. This yields:
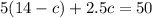
Distribute:
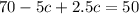
Combine Like Terms:
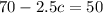
Subtract 70 from both sides:
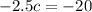
Divide both sides by -2.5:
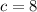
Therefore, Kate gave 8 children’s haircuts.
This means that she gave
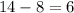 adult haircuts.
adult haircuts.
So, our answer is D. She gave 8 children’s haircuts.