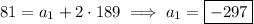Question

A3 = 81 and a6 =648 what is the 1st term?​

Answer 1

The answer depends on what you know about the sequence
`a_n`...

If
`a_n` is geometric, then

`a_n=ra_(n-1)`

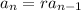
for some fixed number r. Using this recursive rule, we get

`a_(n-1)=ra_(n-2)\implies a_n=r^2a_(n-2)`

`a_(n-2)=ra_(n-3)\implies a_n=r^3a_(n-3)`

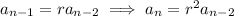
and so on, down to the 1st term in the sequence:

`a_n=r^(n-1)a_1`

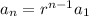
This means

`a_3=81=r^2a_1`

`a_6=648=r^5a_1`

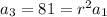
so that

`(648)/(81)=(r^5a_1)/(r^2a_1)\implies 8=r^3\implies r=2`

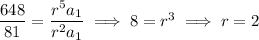
Now solve for
`a_1`:

`81=2^2a_1\implies a_1=\boxed{\frac{81}4}`

If instead
`a_n` is arithmetic, then

`a_n=a_(n-1)+d`

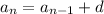
for some fixed number d. Similarly, we can get the n-th number in the sequence in terms of the 1st one:

`a_(n-1)=a_(n-2)+d\implies a_n=a_(n-2)+2d`

`a_(n-2)=a_(n-3)+d\implies a_n=a_(n-3)+3d`

and so on, down to

`a_n=a_1+(n-1)d`

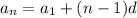
Then

`a_3=81=a_1+2d`

`a_6=648=a_1+5d`

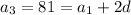
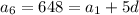
Solve for d :

`(a_1+5d)-(a_1+2d)=648-81\implies 3d=567\implies d=189`

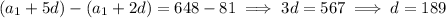
Now solve for
`a_1`:

`81=a_1+2\cdot189\implies a_1=\boxed{-297}`