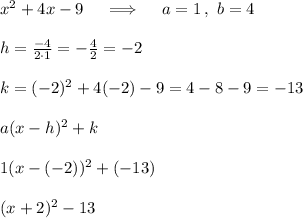Answer:
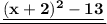
Explanation:
You can do it by completing the square:
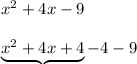
We add 4 to complete the square but we also subtract 4 because we don't want to change the equation (+4-4=0 so it doesn't change anything in equation)
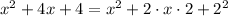
so we get:
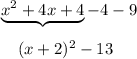
The vertex is: (-2, -13)
(because x+2=x-h ⇒h=-2 and +q=-13 ⇒ q=-13)
We can also use that:
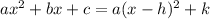 for
for