Question

Someone please please help i am so bad at this and please explain.
you can zoom in if needed

Answer 1

Parts (a) and (b) are functions since they pass the vertical line test.

Part (c) is not a function. It fails the vertical line test since it is possible to pass a single vertical line through more than one point on the curve. In other words, some x input leads to more than one y output. A function can only have one output for any given input.

--------------------

The domain of part (a) is the set of all real numbers. We can plug in any value for x. The domain in interval notation is (-infinity, infinity) as this describes the entire real number line. The domain is the set of all possible inputs.

The range for part (a) is the set of y values such that
`1 \le y \le 3` because the lowest points are when y = 1 and the highest points are when y = 3. The range is the set of all possible outputs. The range in interval notation is [1, 3]. Note the use of square brackets to include the endpoint.

----------------------

The domain for part (b) is also the set of real numbers. The reasoning is the same as part (a).

The range of part (b) is
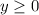`y \ge 0` since y = 0 is the lowest y possible output, and there is no largest output y value. The range in interval notation is [0, infinity).

----------------------

The domain of part (c) is different from the others. On this graph, the left-most point is when x = -2, so the domain is the set of real x values such that
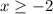`x \ge -2` which translates to [-2, infinity) in interval notation.

The range of part (c) is the set of all real numbers. Any y value is a possible output because the parabola stretches upward and downward forever.