Question

Can someone help the lesson is about ordering.​

Answer 1

Answer:
`3 \le x \le 5`

x is any real number between 3 and 5, including both endpoints

================================================

Step-by-step explanation:

If A < B, then 1/A > 1/B. Applying the reciprocal flips the inequality sign.

For example, if 2 < 3, then 1/2 > 1/3. It might help to look at the decimal representations

1/2 = 0.500

1/3 = 0.333

We see that 1/2 is larger.

-----------

The inequality
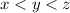`x < y < z` is the same as
`x < y \ \text{ and } \ y < z`.

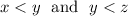We've broken the single inequality into two smaller parts.

The given inequality breaks down into
`(1)/(6) \le (1)/(x+1)` and
`(1)/(x+1) \le (1)/(4)`

------------

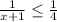
Let's solve the first inequality for x

`(1)/(6) \le (1)/(x+1)\\\\6 \ge x+1\\\\6-1 \ge x\\\\5 \ge x\\\\x \le 5`

Repeat for the other inequality as well

`(1)/(x+1) \le (1)/(4)\\\\x+1 \ge 4\\\\x \ge 4-1\\\\x \ge 3\\\\`

-------------------------

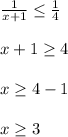
We found that
`x \ge 3 \ \text{ and } \ x \le 5`

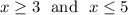
This is the same as
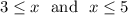`3 \le x \ \text{ and } \ x \le 5` which combines to
`3 \le x \le 5`