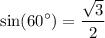Question

In the adjoining equilateral
`\triangle` ABC , AD ⊥ BC and AC = 2a units. Prove that sin 60° =
`\sf{ ( √( 3) )/(2) }` .

Answer 1

See Below.

Explanation:

Since ΔABC is an equilateral triangle, this means that ∠A, ∠B, and ∠C all measure 60°.

Furthermore, all sides of the triangle measure 2a.

We know that AD⊥BC. Since this is an equilateral triangle, any altitude will be a perpendicular bisector. Therefore, BD = DC, ∠CAD = 30° and ∠C = 60°.

Additionally, the measures of the segments are: BD = DC = (2a) / 2 = a.

Let’s use the right triangle on the right. Here, we have that DC = a and AC = 2a.

Recall that sine is the ratio of the opposite side to the hypotenuse. Therefore, sin(C) or sin(60°) will be AD / AC. We can find AD using the Pythagorean Theorem:

`a^2+b^2=c^2`

a is DC, b is AD, and c is AC.

Substitute in appropriate values:

`a^2+(AD)^2=(2a)^2`

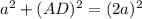
Solve for AD:

`\displaystyle \begin{aligned} a^2+(AD)^2&=4a^2\\(AD)^2&=3a^2\\AD&=√(3a^2)=a√(3)\end{aligned}`

Sine is the ratio of the opposite to the hypotenuse:

`\displaystyle \sin(C)=\sin(60\textdegree)=\frac{\text{opposite}}{\text{hypotenuse}}`

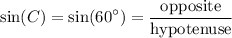
Substitute:

`\displaystyle \sin(60\textdegree)=(AD)/(AC) = (a√(3))/(2a)`

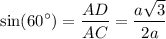
Simplify. Hence, regardless of the value of a:

`\displaystyle \sin(60^\circ)=(\sqrt3)/(2)`