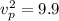Question

A 560-g squirrel with a surface area of falls from a 5.0-m tree to the ground. Estimate its terminal velocity. (Use a drag coefficient for a horizontal skydiver.) What will be the velocity of a 56-kg person hitting the ground, assuming no drag contribution in such a short distance

Answer 1

Complete Question

A 560-g squirrel with a surface area of
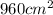`960 cm^2`falls from a 5.0-m tree to the ground. Estimate its terminal velocity. (Use a drag coefficient for a horizontal skydiver.) What will be the velocity of a 56-kg person hitting the ground, assuming no drag contribution in such a short distance

Answer:

The terminal velocity of the 560-g squirrel is
`v  =  9.9 \ m/s`

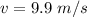
The velocity of the 56-kg person is
`v_p^2 =  9.9`

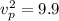
Step-by-step explanation:

From the question we are told that

The mass of the squirrel is
`m_s  =560 \ g  = 0.56 \  kg`

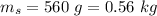
The height of the fall is
`s =  5 \  m`

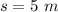
The drag coefficient of a skydiver is is
`C   =  1`

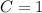
The surface area is
`A =  930 \  cm^2  =  0.093 \ m^2`

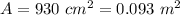
Generally the density of air is
`\rho  =  1.21 \  kg /m^3`

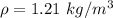
Generally the terminal velocity is mathematically represented as

`v  =  \sqrt{ (2 *  m  *  g)/( \rho *  C  *A ) }`

=>
`v  =  \sqrt{ (2 *  0.56  *  9.8)/(  1.21  *  1 * 0.093  ) }`

=>
`v  =  9.9 \ m/s`

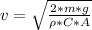
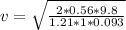
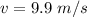
Generally from kinematic equation

`v_p^2 =  u^2 + 2gs`

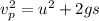
given that the person was at rest before the fall u = 0 m/s

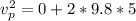
`v_p^2 =  0+ 2* 9.8 * 5`

=>
`v_p^2 =  9.9`