Question

To find the area of this right triangle, Diego and Jada used different strategies. Diego drew a line through the midpoints of the two longer sides, which decomposes the triangle into a trapezoid and a smaller triangle. He then rearranged the two shapes into a parallelogram.

Answer 1

The question is incomplete. Here is the complete question.

To find the area of this right triangle, Diego and Jada used different strategies. Diego drew a line thorugh the midpoints of the two longer sides, which decomposes the triangle into a trapezoid and a smaller triangle. He then rearranged the two shapes into a parallelogram, shown in the first figure below.

Jada made a copy of the triangle, rotated it, and lined it up against one side of the original triangle so that the two triangles make a parallelogram. Second figure below shows Jada's strategy.

1. Explain how Diego might use his parallelogram to find the area of the triangle.

2. Explain how Jada might use his parallelogram to find the area of the triangle.

Answer and Step-by-step explanation: 1. The figure of Diego's strategy shows that the area of the triangle equals the area of the parallelogram.

Area of a parallelogram is calculated as width x height, so:

A = w x h

A = 3 x 4

A = 12

Using Diego's drawings, area of the parallelogram and the triangle is 12ft.

2. In Jada's drawings, the two triangles form a parallelogram, but it wants the area of only half of the parallelogram. Therefore:

A =
`(width X length)/(2)`

A =
`(3*8)/(2)`

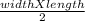
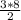
A = 3 x 4

A = 12

According to Jada's plan, area of the triangle is 12ft.