Question

A container consists of a cylinder of diameter 1.4 m and an inverted cone. The height of the container is 3.6 m and it contains water to a depth of 3 m, as shown below. Given that the volume of the water in the container is 2464 litres, find the height of the cylinder. (Take =227)

Answer 1

1.5 m

Explanation:

Given that:

The diameter of the cylinder = 1.4 m

Then the radius will be = 1.4 m/ 2 = 0.7 m = 7dm

Similarly, the height of the container = 3.6 m = 36 dm

Suppose the height of the inverted cone = h_c and the height of the cylinder tube = h_d

Then the tank height = h_c + h_d

36 m = h_c + h_d ------ (1)

However, the volume of the water in the cone can be computed as:

`= (1)/(3) * \pi * r ^ 2 * h_c`

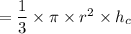
Similarly, the volume of the water in the cylinder tube is:

`= \pi * r ^ 2 * h_d`

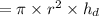
The volume of water in the container = 2.464 liters

Thus;

The volume of water in the cone + volume of water in the tube = volume of water

`( (1)/(3) * \pi * r ^ 2 * h_c )+( \pi * r ^ 2 * h_d) = 2464`

`\pi * r ^ 2 ( (1)/(3) * h_c + h_d) = 2464`

`\pi * 7^ 2 ( (1)/(3) * h_c + 30 - h_c) = 2464`

`154 ( -(2)/(3) h_c + 30 ) = 2464`

`( -(2)/(3) h_c + 30 ) = (2464)/(154)`

`( -(2)/(3) h_c + 30 ) =16`

`( -(2)/(3) h_c ) = 16-30`

`-(2)/(3) h_c =-14`

`h_c =-14 /- (2)/(3)`

`h_c =-7 *-3`

`h_c =21`

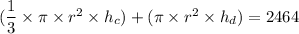
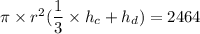
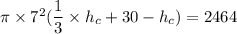
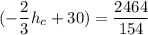
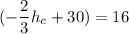
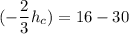
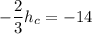
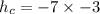
From equation (1):

36 m = h_c + h_d

h_d = 36 - h_c

h_d = 36 - 21

h_d = 15 dm

Therefore, the height of the cylinder tube is 15 dm = 1.5 m