Question

It is known that 50% of adult workers have a high school diploma. If a random sample of 6 adult workers is selected, what is the probability that 3 or more of them have a high school diploma? (That is, find P(X f$displaystyle geq f$ 3) (round to 4 decimal places) Answer:

Answer 1

Answer: 0.6563

Explanation:

Given: The probability that adult workers have a high school diploma : p= 0.50

Sample size : n= 6

Let x be the number of workers have high school diploma.

Binomial distribution formula,

`P(X=x)=\ ^nC_xp^x(1-p)^(n-x)`

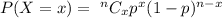
Now, the probability that 3 or more of them have a high school diploma will be:

`P(X\geq3)=1-P(X<2)\\\\=1-(P(X=0)+P(X=1)+P(X=2))\\\\=1-(^6C_0(0.5)^6(1-0.5)^0+^6C_1(0.5)^1(1-0.5)^5+^6C_2(0.5)^2(1-0.5)^4)\\\\=1-((1)(0.5)^6+(6(0.5)(0.5)^5)+(6!)/(2!4!)(0.5)^2(0.5)^4)\\\\=1-(0.015625+0.09375+0.234375)\\\\=1-0.34375\\\\=0.65625\approx0.6563`

Hence, required probability = 0.6563