Question

A cube of edge length 6 cm is sliced into 20 congruent pieces by vertical cuts perpendicular to a base of the cube and parallel to a face. The total surface area of the 20 pieces exceeds the surface area of the original cube by x square centimeters. What is x? (Do NOT include punctuation in your answer.)

Answer 1

The total surface area of the 20 pieces exceeds the surface area of the original cube by 1368 square centimeters.

Explanation:

The formula of surface area for the entire cube (
`A_(s,c)`), measured in square centimeters, is:

`A_(s,c) = 6\cdot l^(2)` (Eq. 1)

Where
`l` is the side length, measured in centimeters.

If this cube is sliced into 20 pieces, the surface area of each slice (
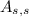`A_(s,s)`), measured in square centimeters, is equal to:

`A_(s,s) = 4\cdot \left((1)/(20)\right)\cdot l^(2)+2\cdot l^(2)`

`A_(s,s) = (1)/(5)\cdot l^(2)+2\cdot l^(2)`

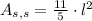`A_(s,s) = (11)/(5)\cdot l^(2)` (Eq. 2)

And the surface area of all slices (
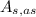`A_(s,as)`), measured in square centimeters, is:

`A_(s,as) = 44\cdot l^(2)` (Eq. 3)

Then, we calculate the excess of surface area (
`\Delta A`), measured in square centimeters, by applying the following formula:

`\Delta A = A_(s,as)-A_(s,c)`

`\Delta A = 44\cdot l^(2)-6\cdot l^(2)`

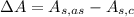
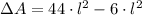
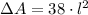`\Delta A = 38\cdot l^(2)` (Eq. 4)

If
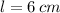`l = 6\,cm`, then the excess of surface area is:

`\Delta A = 38\cdot (6\,cm)^(2)`

`\Delta A = 1368\,cm^(2)`

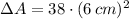
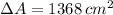
The total surface area of the 20 pieces exceeds the surface area of the original cube by 1368 square centimeters.