Question

An art exhibit at a local museum features several similarly shaped metal cubes welded together to make a sculpture. The smallest cube has a edge length of 6 inches. What are the edge lengths of the other cubes if the ratios of similarity to the smallest cube are 1.25, 43 , 1.5, 74 , and 2 respectively?

Answer 1

Given:

The smallest cube has a edge length of 6 inches.

The ratios of similarity to the smallest cube are 1.25, 43 , 1.5, 74 , and 2 respectively.

To find:

The edge lengths of the other cubes.

Solution:

If two figures are similar, then the ratios of similarity is equal to the ratio of their corresponding sides.

Let the edge of other cube be x.

`\text{Ratio of similarity}=\frac{\text{Edge of other cube}}{\text{Edge of smaller cube}}`

`\text{Ratio of similarity}=(x)/(6)`

`6* \text{Ratio of similarity}=x`

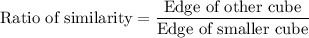
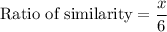
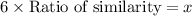
It means, the edges of other cubes are 6 times of the ratio of similarity to the smallest cube.

Now,

`6(1.25)=7.5`

`6((4)/(3))=8`

`6(1.5)=9`

`6((7)/(4))=10.5`

`6(2)=12`

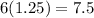
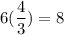
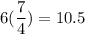
Therefore, the edges of other cubes are 7.5, 8, 9, 10.5 and 12 respectively.