Question

A tower crane has a hoist motor rated at 157 hp. If the crane is limited to using 75.0 % of its maximum hoisting power for safety reasons, what is the shortest time in which the crane can lift a 5650 kg load over a distance of 95.0 m

Answer 1

The shortest time in which the crane can lift a 5650-kg load over a distance of 95 meters is 58.97 seconds.

Step-by-step explanation:

The tower crane uses electric energy to create mechanical energy in the form of rotational kinetic energy, which is transformed in translational kinetic energy by means of cables, gear boxes and pulleys. For this exercise we consider the 5650-kg load as our system, which needs to overcome gravity to be lifted over a distance of 95 meters.

If load is moved at constant speed, then the power needed to lift that load is reduced to a change in gravitational potential energy based on Principle of Energy Conservation and Energy-Work Theorem. That is:

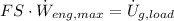`FS\cdot \dot W_(eng, max) = \dot U_(g, load)` (Eq. 1)

Where:

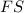`FS` - Factor of safety of the hoist motor, dimensionless.

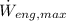`\dot W_(eng, max)` - Maximum hoisting power, measured in watts.

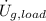`\dot U_(g, load)` - Rate of change of the gravitational potential energy of the load, measured in watts.

By applying the definition of potential energy and assuming no changes in mass of the system, we expand the formula as follows:

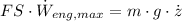`FS\cdot \dot W_(eng,max) = m\cdot g\cdot \dot z` (Eq. 2)

Where:

`m` - Mass of the load, measured in kilograms.

`g` - Gravitational acceleration, measured in meters per square second.

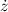`\dot z` - Ascension rate of the load, measured in meters per second.

Now we clear the ascension rate within expression:

`\dot z = (FS\cdot \dot W_(eng,max))/(m\cdot g)`

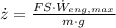
If we know that
`FS = 0.75`,
`\dot W_(eng, max) = 117122\,W`,
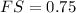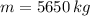`m = 5650\,kg` and
`g = 9.807\,(m)/(s^(2))`, then the ascension rate of the load is:

`\dot z = (0.75\cdot (117122\,W))/((5560\,kg)\cdot \left(9.807\,(m)/(s^(2)) \right))`

`\dot z = 1.611\,(m)/(s)`

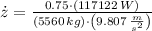
From Kinematics, the shortest time possible is calculated by means of this formula:

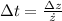`\Delta t = (\Delta z)/(\dot z)` (Eq. 3)

Where:

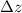`\Delta z` - Lift distance, measured in meters.

`\Delta t` - Shortest time, measured in seconds.

Lastly, if we get that
`\dot z = 1.611\,(m)/(s)` and
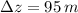`\Delta z = 95\,m`, then time needed to lift 5650-kg load over a distance of 95 meters is:

`\Delta t = (95\,m)/(1.611\,(m)/(s) )`

`\Delta t = 58.97\,s`

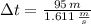
The shortest time in which the crane can lift a 5650-kg load over a distance of 95 meters is 58.97 seconds.