Answer:
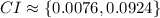
Explanation:
The formula for a z-confidence interval for a difference of proportions is
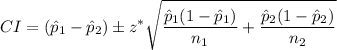 :
:
Let
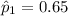 to represent the sample proportion of
to represent the sample proportion of
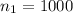 women who are in favor of stricter gun control laws and let
women who are in favor of stricter gun control laws and let
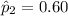 to represent the sample proportion of
to represent the sample proportion of
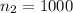 men who are in favor of stricter gun control laws.
men who are in favor of stricter gun control laws.
A 95% confidence level corresponds to a critical value of
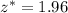 , so now we perform the necessary calculations assuming conditions are met:
, so now we perform the necessary calculations assuming conditions are met:
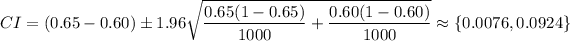
Hence, we are 95% confident that the true difference in the proportion of women and men who favor stricter gun control laws is between 0.0076 and 0.0924
Since the interval does not contain "0" and only contain values greater than "0", it is more likely that the proportion of women who were in favor of stricter gun control laws is higher than the proportion of men who were in favor of stricter gun control laws.