Question

Number 6 please! Ty!!

Answer 1

Explanation:

Hey there!

The equation of a line passes through point (-2,2) is;

(y-2) = m1(X+2).............(i)

Another equation is;

y= 2/3x +2............ (ii)

From equation (ii)

y = 2/3x+2

Comparing the equation with y= mx+c, we get;

Slope(M2) = 2/3.

For perpendicular lines the condition is; M1*M2= -1

So, let's find M1 here.

`m1 * (2)/(3) = - 1`

`2m1 = - 3`

`m1 = ( - 3)/(2)`

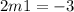
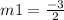
Therefore, M1= -3/2.

Putting the value of M1 in equation (i), we get;

`(y - 2) = - (3)/(2) (x + 2)`

`(y - 2) = - (3)/(2) x + 2 * - (3)/(2)`

`(y - 2) = - (3)/(2) x - 3`

`y = - (3)/(2) x - 1`

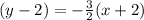
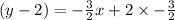
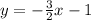
Therefore, the equation is y= -3/2x-1.

Hope it helps...