Question

Zinc metal is added to hydrochloric acid to generate hydrogen gas and is collected over a liquid whose vapor pressure is the same as that of pure water at 20.0°C (18 torr). The volume of the mixture is 1.7 L, and its total pressure is 0.788 atm. Determine the number of moles of hydrogen gas present in the sample.

Answer 1

About 0.054 moles.

Step-by-step explanation:

Apply the ideal gas law. Recall that:

`\displaystyle PV = n RT`

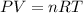
Solve for n, the number of moles:

`\displaystyle n = (PV)/(RT)`

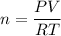
Determine the pressure of the hydrogen gas. Recall that by Dalton's Law of Partial Pressures, the total pressure is equal to the sum of the partial pressures of each individual gas:

`\displaystyle P_T = P_\ell + P_\text{H$_2$}`

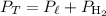
Convert the vapor pressure of the liquid to atm (1.00 atm = 760. torr):

`\displaystyle 18\text{ torr} \cdot \frac{1.00\text{ atm}}{760.\text{ torr}} = 0.024\text{ atm}`

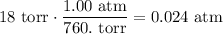
Therefore, the partial pressure of the hydrogen gas is:

`\displaystyle \begin{aligned} P_T & = P_\ell + P_\text{H$_2$} \\ \\ (0.788\text{ atm}) & = (0.024\text{ atm}) + P_\text{H$_2$} \\ \\ P_\text{H$_2$} & = 0.764\text{ atm}\end{aligned}`

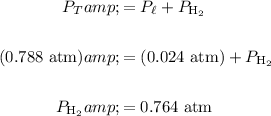
Therefore, the number of moles of hydrogen gas present is (the temperature in kelvins is 273.15 + 20.0 = 293.2 K):

`\displaystyle \begin{aligned} n & = (PV)/(RT) \\ \\ & = \frac{(0.764\text{ atm})(1.7\text{ L})}{\left(0.08206 \text{ }\frac{\text{L-atm}}{\text{mol-K}}\right)(293.2\text{ K})}\\ \\ & = 0.054\text{ mol H$_2$} \end{aligned}`