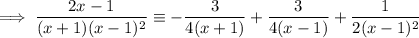Answer:
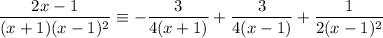
Explanation:
When writing an algebraic fraction as an identity, if its denominator has repeated linear factors, the power of the repeated factor indicates how many times that factor should appear in the partial fractions. A factor that is squared in the original denominator will appear in the denominator of two partial fractions - once squared and once without the square.
Write out the fraction as an identity:
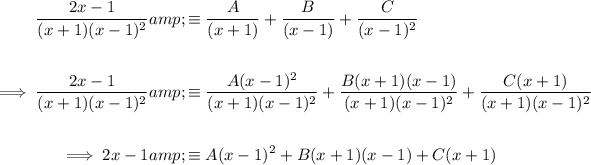
Calculate the values of A and C using substitution:
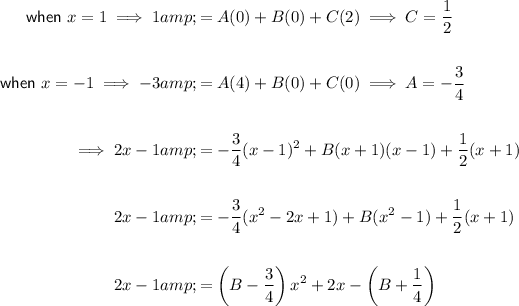
Compare constants to find B:
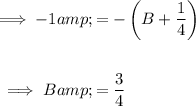
Replace the found values of A, B and C in the original identity: