Question

Monochromatic electromagnetic radiation illuminates an area of a surface. The electric and magnetic fields of the waves are then doubled in magnitude. How is the total energy incident on the surface per unit time affected by this increase in the electric and magnetic fields

Answer 1

Complete Question

Monochromatic electromagnetic radiation illuminates an area of a surface. The electric and magnetic fields of the waves are then doubled in magnitude. How is the total energy incident on the surface per unit time affected by this increase in the electric and magnetic fields?

(a) The total energy is not affected by this change.

(b) The total energy will increase by a factor of two.

(c) The total energy will increase by a factor of four.

(d) The total energy will decrease by a factor of two.

(e) The total energy will decrease by a factor of four.

Answer:

(c) The total energy will increase by a factor of four.

Step-by-step explanation:

Generally the total energy is directly proportional to the square of the amplitude of the (electric and magnetic field of the wave ) , this can be mathematically represented as

`E  \ \ \alpha \ \ A^2`\

=>
`E = k  A^2`

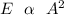Here k is a constant

=>
`k = (E)/(A^2)`

=>
`(E_1)/(A_1^2)  = (E_2)/(A_2^2)`

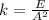
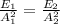
Now when the amplitude of( electric and magnetic fields) are doubled, i.e when
`A_2 =  2A_1`

`(E_1)/(A_1^2)  = (E_2)/((2A_1)^2)`

=>
`(E_1)/(A_1^2)  = (E_2)/( 4 A_1^2)`

=>
`E_2 =  4 E_1`

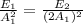
So we see that the total energy increase by