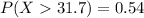Question

. Let the random variable P be the air pressure in a car tire, and assume that P is uniformly distributed between 29 and 34 pounds per square inch (psi). Recall that this means that the density curve for P is a flat, horizontal line at some constant level c above the interval from 29 psi to 34 psi. (a) Find the probability that the pressure of a tire will be above 31.7 psi.

Answer 1

The probability is
`P(X >  31.7) = 0.54`

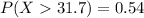
Explanation:

From the question we are told that

P is uniformly distributed between
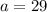`a=  29` and
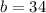`b=34` pounds per square inch (psi)

Generally the uniform distribution cumulative distribution function is mathematically represented as

`F(x ) =  \left \{ {{ 0  \\ \ \ \ \ \  x \le a} \atop { (x-a)/(b-a) \ \ \ \ \ \ \ \ a <  x < b}}  \atop {1 \ \ \ \ \ \ \ \ \ \ \ \ \ x \ge  b}} \right.`

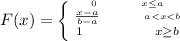
Generally the probability that the pressure of a tire will be above 31.7 psi

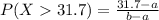
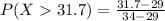
`P(X >  31.7) =  ( 31 . 7  -  a )/(b-a)`

=>
`P(X >  31.7) =  ( 31 . 7  -  29 )/(34-29)`

=>
`P(X >  31.7) = 0.54`