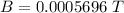Question

A beam of protons is directed in a straight line along the positive zz ‑direction through a region of space in which there are crossed electric and magnetic fields. If the electric field magnitude is E=450E=450 V/m in the negative yy ‑direction and the protons move at a constant speed of v=7.9×105v=7.9×105 m/s, what must the direction and magnitude of the magnetic field be in order for the beam of protons to continue undeflected along its straight-line trajectory? Select the direction of the magnetic field BB .

Answer 1

The magnitude is
`B = (450)/(7.9* 10^5)`

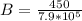
The direction is the positive x axis

Step-by-step explanation:

From the question we are told that

The electric field is E = 450 V/m in the negative y ‑direction

The speed of the proton is
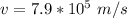`v= 7.9* 10^5\  m/s` in the positive z direction

Generally the overall force acting on the proton is mathematical represented as

`F_E =  q(\vec E + \vec v  * \vec B)`

Now for the beam of protons to continue un-deflected along its straight-line trajectory then
`F_E =0`

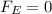
So

`0  =  q( E (-y) + v(z)  * \vec B)`

=>
`E\^y = v \^ z  * \vec B`

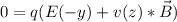
Generally from unit vector cross product vector multiplication

`\^ z  \ *  \  \^ x  =  \^  y`

So the direction of B (magnetic field must be in the positive x -axis )

So

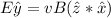
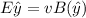
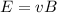
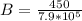
`E\^y = v \^ z  *  B\^ x`

=>
`E\^y = vB ( \^ z  *  \^ x)`

=>
`E\^y = vB ( \^y)`

=>
`E = vB`

=>
`B = (450)/(7.9* 10^5)`

=>
`B =  0.0005696 \ T`