Question

Sketch the region enclosed by the given curves.

y = tan(9x), y = 2 sin(9x), −π/27 ≤ x ≤ π/27

Find its area.

Answer 1

Area (A)
`\simeq` 0.0682

Explanation:

The sketch for the region enclosed by the given curves can be found in the image attached below.

From the image below;

The two curves intersect in the area of tan 9x = 2 sin 9x

Recall that:

`(sin \ 9x )/(cos \ 9x ) = 2 \ sin \ 9x`

`cos \ 9 x= (1)/(2)`

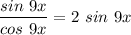
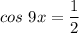
making x the subject; then:

`x = (1)/(9) cos ^(-1)((1)/(2))`

`x = (1)/(9)((\pi)/(3))`

`x = (\pi)/(27)`

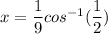
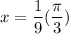
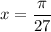
The subdivision of the domain is in two intervals
`[-(\pi)/(27), 0], [0, (\pi)/(27)]`

where;

`x \ \ \varepsilon \ \ [ -(\pi)/(27),0]; tan \ 9x > 2 sin \ 9x`

`x \ \ \varepsilon \ \ [ 0,(\pi)/(27)]; tan \ 9x < 2 \ sin \ 9x`

Area (A) =
`\int ^0_(-\pi/27)}} ( tan \ 9x - 2 \ sin \ 9x ) \ dx + \int ^(\pi/27)_(0)(2 \ sin \ 9x - tan \ 9x \ ) \ dx`

`= \begin {bmatrix} (1)/(9) In \ sec 9x + (2)/(9) \ cos \ 9x \end {bmatrix}^0_(-\pi/27) + \begin {bmatrix} -(2)/(7) cos 9x - (1)/(9) \ In \ sec \ 9x \end {bmatrix}^(-\pi/27) _0`

`= (1)/(9)(1-In 2) + (1)/(9)(1-In 2)\\`

`= (2)/(9)(1 - In 2)`

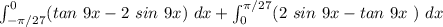
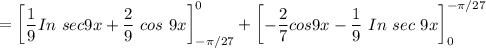
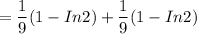
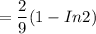
Area (A) = 0.06818

Area (A)
`\simeq` 0.0682