Question

A line passes through the points (−4,−9)

and (−2,−6) What is the equation of the line in Slope-Intercept Form?

Answer 1

The equation of the line in slope-intercept form that passes through the points (-4, -9) and (-2, -6) is y = 1.5x - 3.

Step-by-step explanation:

In Mathematics

, the equation of a line can be determined using the

Slope-Intercept Form

which is expressed as y = mx + c, where 'm' represents the slope of the line and 'c' is the y-intercept.

To calculate the slope (m), we use the formula: m = (y2 - y1) / (x2 - x1). Plugging in the values of your points which are (-4, -9) as (x1, y1) and (-2, -6) as (x2, y2), we get: m = (-6 - (-9)) / (-2 - (-4)) = 1.5.

Once we have the slope, we can find the y-intercept 'c' by rearranging the line equation to: c = y - mx and substituting in the values of one of the points and the slope (let's use first point (-4, -9)). Thus, c = -9 - 1.5*-4 = -3.

Therefore, our final equation of the line in slope-intercept form is: y = 1.5x - 3.

Learn more about Slope-Intercept Form

Answer 2

D.
`y - 5= 3(x - 1)`

B.
`y = (3)/(2)x - 3`

Step-by-step explanation:

Problem 1:

Point-slope form equation is given as
`y - y_1 = m(x - x_1)`, where, (x1, y1) is a point on the line, and m = slope.

Find the slope of the line of the graph given, using 2 points on the line, points (0, 2) and (1, 5).

`m = (y_2 - y_1)/(x_2 - x_1) = (2 - 5)/(0 - 1) = (-3)/(-1) = 3`

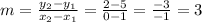
Substitute (x1, y1) = (1, 5) and m = 3 into
`y - y_1 = m(x - x_1)`

`y - 5= 3(x - 1)`

The answer is D.

Problem 2:

Slope-intercept equation takes the form:
`y = mx + b`, where, m = slope, and b = y-intercept.

Find m and b.

Given, points (−4,−9) and (−2,−6),

`slope(m) = (y_2 - y_1)/(x_2 - x_1) = (-6 -(-9))/(-2 -(-4)) = (3)/(2) = (3)/(2)`

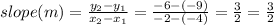
Substitute x = -2, y = -6, and m = ³/2 into
`y = mx + b`, to find b:

`-6 = (3)/(2)(-2) + b`,

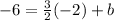Subtract b from both sides

`-6 = -3 + b`

Add 3 to both sides

`-6 + 3 = b`

`-3 = b`

`b = -3`

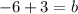
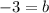
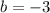
Substitute m = ³/2, b = -3 into
`y = mx + b`

`y = (3)/(2)x + (-3)`

`y = (3)/(2)x - 3`

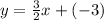
The answer is B.