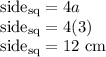Answer:
Length of the side of the square is 12 cm.
Explanation:
Given information:

Our mission is to find the length of the side of the square. We know that the side of the square is 4a cm, so to be able to answer we have to find the value of a first.
Step 1: Finding the value of a
Key to finding the value of a is the perimeter of the rectangle. Notice that we can calculate the perimeter of the rectangle in two different ways.
One way was given in the question:

We want equations in terms of a, so we can calculate a. Perimeter of the square can be calculated as:

Substituting the values in equation:
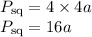
Therefore the first equation for perimeter of the rectangle becomes:

For the second way we use formula for the perimeter of rectangle which is:
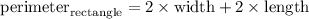
Substituting the values in equation:
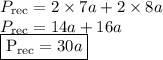
Now let's equate both perimeters of the rectangle.
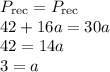
Step 2: Find the length of the side of the square
It's given that side of the square is 4a cm. All we have to do is substituting a with its value, which we got in the previous step.