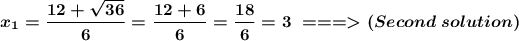Answer:
The quadratic equation 3x² - 12x + 9 = 0 has two real roots when solved:
x₁ = 1 and x₂ = 3
Explanation:
✍ An equation of type ax² + bx + c = 0, can be solved, for example, using the quadratic formula:
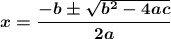
either
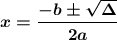
where
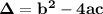
Identify the coefficients
a = 3, b = -12 and c = 9
Calculate the discriminant value
Δ = b² - 4ac
Δ = (-12)² - 4.3.9 = 144 - 12.9
Δ = 144 - 108 = 36
Enter the values of a, b and the discriminant value in the quadratic formula
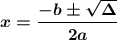
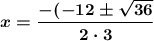
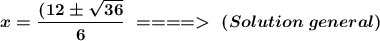
As we can see above, the discriminant (Δ) of this equation is positive (Δ> 0) which means that there are two real roots (two solutions), x₁ and x₂.
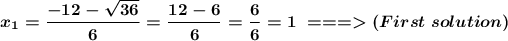
To find x₁, just choose the positive sign before the square root. Later,