Question

What are the coordinates of the image of the point (1-, 2) under a dilation of 3 with the origin

Answer 1

The image of the point (1, -2) under a dilation of 3 is (3, -6).

Explanation:

Correct statement is:

What are the coordinates of the image of the point (1, -2) under a dilation of 3 with the origin.

From Linear Algebra we get that dilation of a point with respect to another point is represented by:

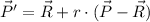`\vec P' = \vec R + r\cdot (\vec P-\vec R)` (Eq. 1)

Where:

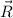`\vec R` - Reference point with respect to origin, dimensionless.

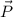`\vec P` - Original point with respect to origin, dimensionless.

`r` - Dilation factor, dimensionless.

If we know that
`\vec R = (0,0)`,
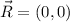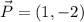`\vec P = (1, -2)` and
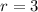`r = 3`, then the coordinates of the image of the original point is:

`\vec P' = (0,0) +3\cdot [(1,-2)-(0,0)]`

`\vec P' = (0,0) + 3\cdot (1,-2)`

`\vec P' = (3,-6)`

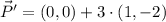
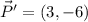
The image of the point (1, -2) under a dilation of 3 is (3, -6).