Question

) A 1000-gallon tank currently contains 100.0 gallons of liquid toluene and a gas saturated with toluene vapor at 85°F and 1 atm. (a) What quantity of toluene (lbm) will enter the atmosphere when the tank is filled and the gas displaced? (b) Suppose that 90% of the displaced toluene is to be recovered by compressing the displaced gas to a total pressure of 5 atm and then cooling it isobarically to a temperature T(°F). Calculate T.

Answer 1

A) m
`_(T)` = 0.3025 * 0.0476 * 92.13 = 1.327 Ibm

B) T= 63.32°F

Step-by-step explanation:

Given data:

1000 gallon tank currently contains 100.0 gallons of liquid toluene

and A gas saturated with toluene vapor at 85°F and 1 atm

A) Calculate quantity of toluene ( Ibm ) that will enter the atmosphere when the tank is filled

m
`_(T)` =
`n_(gas) * Y_(T) * M_(T)`

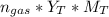
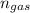`n_(gas)` (total mole of gas) = 0.3025 Ib-mole ( calculated using :
`(PV)/(RT)` )

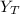`Y_(T)` (mole fraction of toluene) = 0.0476 ( calculated using
`(P_(T) )/(P)` )

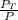M
`_(T)` = 92.13 Ibm/Ib-mole

therefore: m
`_(T)` = 0.3025 * 0.0476 * 92.13 = 1.327 Ibm

B) using Antoine equation to solve for T

Antoine equation :
`log_(10) (P_(T) ) = A - (B)/(T+C)`

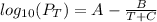
PT( partial pressure ) = 18.95 ( calculated using :
`y_(tb) * P` )

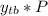A = 6.95805

B = 1346.773

T = ?

C = 219.693

to calculate T make T the subject the subject of the equation

T + 219.693 = 1346.773 / 5.68044

∴ T = 17.40°C

convert T to Fahrenheit

T = 1.8 * 17.40 +32

= 63.32°F