Answer:
The decision rule is
Fail to reject the null hypothesis
The conclusion is
There is no sufficient evidence to accept the manufacturing company claims
Explanation:
From the question we are told that
The sample size is n = 35
The sample standard deviation is
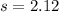
The level of significance is

The null hypothesis is
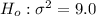
The alternative hypothesis is
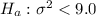
Gnerally the test statistics is mathematically represented as
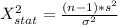
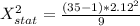
=>

Generally the degree of freedom is mathematically represented as
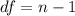
=>
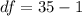
=>
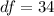
From the chi - distribution table the critical value of
 at a degree of freedom of
at a degree of freedom of
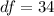 is
is
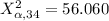
From the value obtained we see that the test statistics does not lie within the region of rejection (1.e 56.060 ,
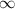 )
)
Then
The decision rule is
Fail to reject the null hypothesis
The conclusion is
There is no sufficient evidence to accept the manufacturing company claims