Explanation:
Let the initial population of a community be P0 and the population after time t is P(t).
If the population of a community is known to increase at a rate proportional to the number of people present at time t, this is expressed as:
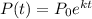
at t = 5 years, P(t) = 2P0
substitute:

If the population is 9,000 after 3 years
at t = 3, P(t) = 9000
a) Substitute into the formula to get P0
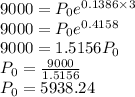
Hence the initial population is approximately 5938.
b) In order to know how fast the population growing at t = 10, we will substitute t = 10 into the formula as shown:
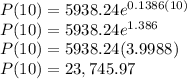
Hence the population of the community after 10 years is approximately 23,746