Question

QUESTION 10

An archer fires an arrow towards a tree with initial speed 65 m/s and angle 25 degrees above the horizontal. If the arrow takes 0.85

seconds to hit the tree, calculate the horizontal distance between the archer and the tree.


QUESTION 11


A monkey throws a banana from a tree into a nearby river. The banana has initial speed 7.6 m/s, is angled 40 degrees below the

horizontal, and takes 0.75 seconds to land in the river. Calculate the speed of the banana when it hits the water.

Answer 1

10) The distance between the archer and the tree is 50.074 meters.

11) The speed of the banana when it hits the water is approximately 13.554 meters per second.

Step-by-step explanation:

10) The arrow experiments a parabolic motion, which is the combination of horizontal motion at constant velocity and vertical uniform accelerated motion. In this case we need to find the horizontal distance between the archer and the tree, calculated by the following kinematic equation:

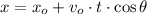`x = x_(o) +v_(o)\cdot t \cdot \cos \theta` (Eq. 1)

Where:

`x_(o)` - Initial position of the arrow, measured in meters.

`x` - Final position of the arrow, measured in meters.

`v_(o)` - Initial speed of the arrow, measured in meters per second.

`t` - Time, measured in seconds.

`\theta` - Launch angle, measured in sexagesimal degrees.

If we know that
`x_(o) = 0\,m`,
`v_(o) = 65\,(m)/(s)`,
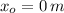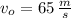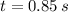`t = 0.85\,s` and
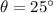`\theta = 25^(\circ)`, the horizontal distance between the archer and the tree is:

`x = 0\,m + \left(65\,(m)/(s)\right)\cdot (0.85\,s)\cdot \cos 25^(\circ)`

`x = 50.074\,m`

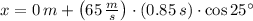
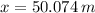
The distance between the archer and the tree is 50.074 meters.

11) The final speed of the banana (
`v`), measured in meters per second, just before hitting the water is determined by the Pythagorean Theorem:

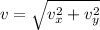`v = \sqrt{v_(x)^(2)+v_(y)^(2)}` (Eq. 2)

Where:

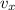`v_(x)` - Horizontal speed of the banana, measured in meters per second.

`v_(y)` - Vertical speed of the banana, measured in meters per second.

Each component of the speed are obtained by using these kinematic equations:

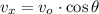`v_(x) = v_(o)\cdot \cos \theta` (Eq. 3)

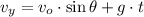`v_(y) = v_(o)\cdot \sin \theta +g\cdot t` (Eq. 4)

Where
`g` is the gravitational acceleration, measured in meters per square second.

If we know that
`v_(o) = 7.6\,(m)/(s)`,
`\theta = -40^(\circ)`,
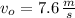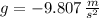`g = -9.807\,(m)/(s^(2))` and
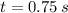`t = 0.75\,s`, the components of final speed are, respectively:

`v_(x) = \left(7.6\,(m)/(s) \right)\cdot \cos (-40^(\circ))`

`v_(x) = 5.822\,(m)/(s)`

`v_(y) = \left(7.6\,(m)/(s)\right)\cdot \sin (-40^(\circ))+\left(-9.807\,(m)/(s^(2)) \right) \cdot (0.75\,s)`

`v_(y) = -12.240\,(m)/(s)`

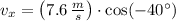
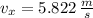
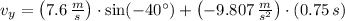
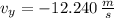
And the speed of the banana right before hitting the water is:

`v = \sqrt{\left(5.822\,(m)/(s) \right)^(2)+\left(-12.240\,(m)/(s) \right)^(2)}`

`v \approx 13.554\,(m)/(s)`

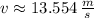
The speed of the banana when it hits the water is approximately 13.554 meters per second.